Theo thống kê từ baogiaoduc24h.com, hình học không gian và đặc biệt là chủ đề về đường thẳng song song với mặt phẳng luôn là một trong những nội dung quan trọng trong chương trình toán học phổ thông. Bài viết này sẽ giúp các bạn học sinh hiểu rõ hơn về khái niệm và ứng dụng của đường thẳng song song với mặt phẳng.
Khái Niệm Cơ Bản Về Đường Thẳng Song Song Với Mặt Phẳng
Định Nghĩa
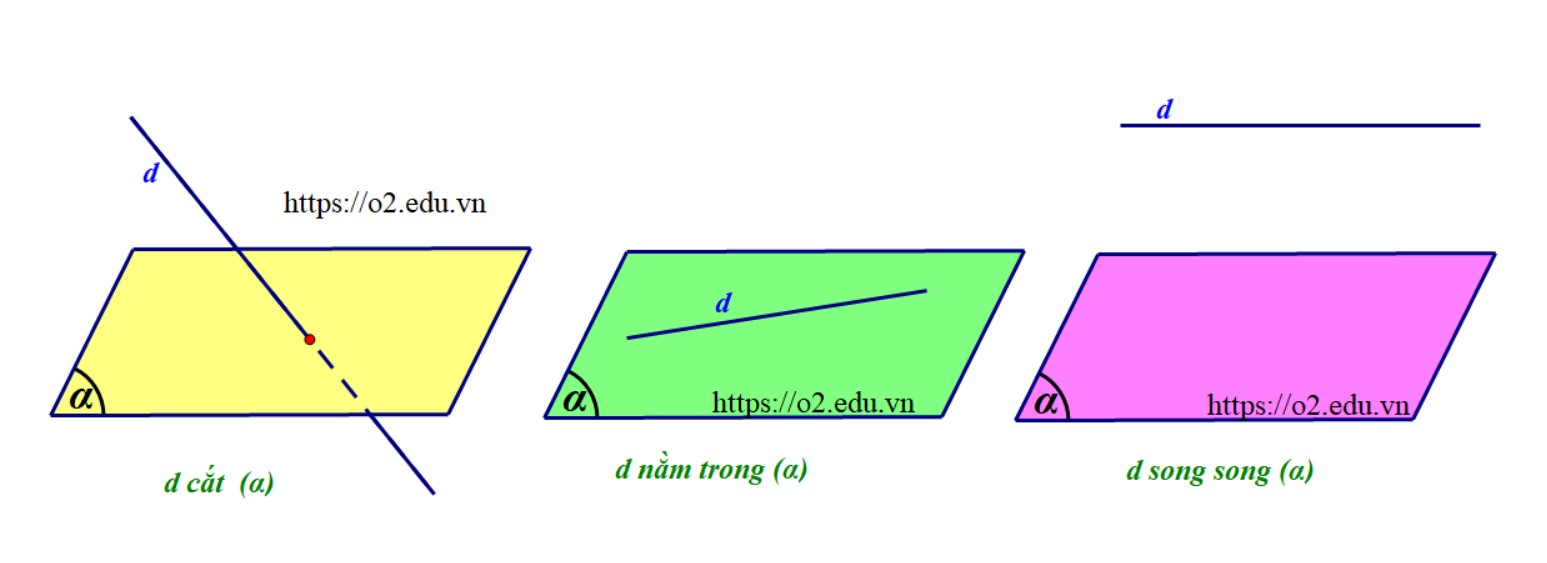
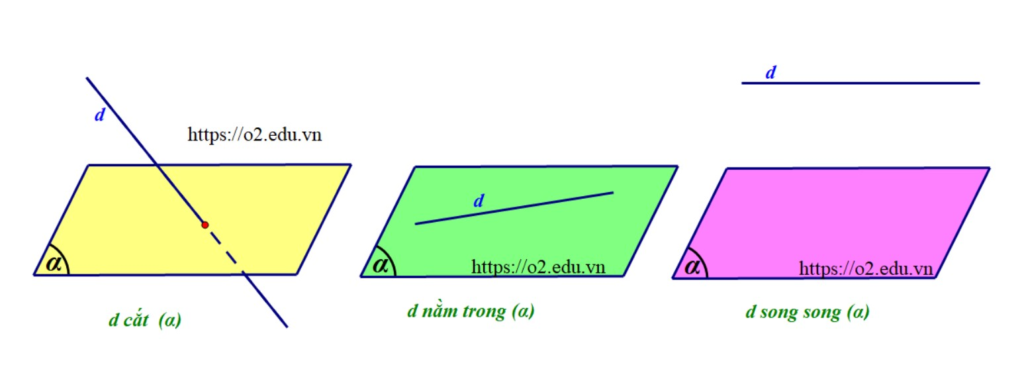
Một đường thẳng được gọi là song song với một mặt phẳng khi đường thẳng đó không có điểm chung với mặt phẳng. Trong không gian ba chiều, đây là một khái niệm quan trọng giúp chúng ta hiểu được mối quan hệ giữa các đối tượng hình học.
Đặc Điểm Nhận Dạng
Để xác định một đường thẳng song song với mặt phẳng, ta cần chú ý những đặc điểm sau:
- Đường thẳng và mặt phẳng không có điểm chung
- Khoảng cách từ một điểm bất kỳ trên đường thẳng đến mặt phẳng là không đổi
- Véc tơ chỉ phương của đường thẳng song song với mặt phẳng
Điều Kiện Để Đường Thẳng Song Song Với Mặt Phẳng
Điều Kiện Véc Tơ
Một đường thẳng song song với mặt phẳng khi và chỉ khi véc tơ chỉ phương của đường thẳng song song với mặt phẳng đó. Điều này có nghĩa là véc tơ chỉ phương của đường thẳng phải vuông góc với véc tơ pháp tuyến của mặt phẳng.
Điều Kiện Tọa Độ
Trong hệ tọa độ không gian Oxyz, nếu mặt phẳng (P) có phương trình ax + by + cz + d = 0 và đường thẳng (d) có phương trình tham số:
x = x₀ + mt
y = y₀ + nt
z = z₀ + ptThì điều kiện để đường thẳng (d) song song với mặt phẳng (P) là:
- am + bn + cp = 0 (điều kiện véc tơ chỉ phương)
- ax₀ + by₀ + cz₀ + d ≠ 0 (điều kiện không có điểm chung)
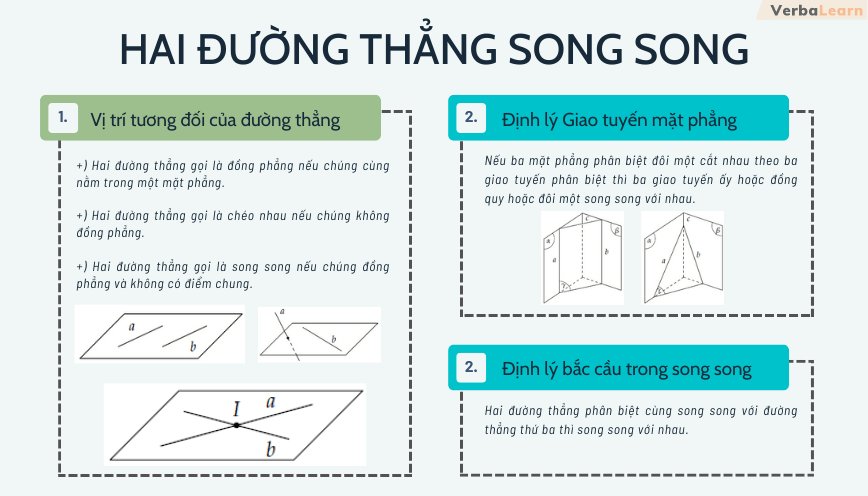
Các Dạng Bài Tập Thường Gặp
Dạng 1: Chứng Minh Đường Thẳng Song Song Với Mặt Phẳng
Đây là dạng bài tập cơ bản nhất, yêu cầu học sinh:
- Xác định véc tơ chỉ phương của đường thẳng
- Xác định véc tơ pháp tuyến của mặt phẳng
- Chứng minh hai véc tơ này vuông góc với nhau
Dạng 2: Tìm Điều Kiện Để Đường Thẳng Song Song Với Mặt Phẳng
Trong dạng bài này, học sinh cần:
- Viết phương trình của đường thẳng và mặt phẳng
- Áp dụng điều kiện véc tơ và điều kiện không có điểm chung
- Giải hệ phương trình để tìm điều kiện
Dạng 3: Tính Khoảng Cách
Khoảng cách từ một điểm đến mặt phẳng là một ứng dụng quan trọng, được tính theo công thức:
d = |ax₀ + by₀ + cz₀ + d| / √(a² + b² + c²)Ứng Dụng Trong Thực Tế
Trong Kiến Trúc
Kiến thức về đường thẳng song song với mặt phẳng được ứng dụng rộng rãi trong:
- Thiết kế các công trình xây dựng
- Lắp đặt hệ thống điện, nước
- Thiết kế nội thất
Trong Công Nghệ
Ứng dụng trong:
- Thiết kế đồ họa 3D
- Lập trình game
- Công nghệ thực tế ảo (VR)
Phương Pháp Giải Bài Tập Hiệu Quả
Bước 1: Phân Tích Đề Bài
- Xác định các yếu tố đã cho
- Xác định yêu cầu cần chứng minh hoặc tính toán
- Vẽ hình minh họa (nếu cần)
Bước 2: Lập Kế Hoạch Giải
- Chọn phương pháp phù hợp
- Xác định các công thức cần sử dụng
- Lập trình tự các bước giải
Bước 3: Thực Hiện Giải
- Áp dụng các công thức đã chọn
- Tính toán cẩn thận
- Kiểm tra kết quả
Lời Khuyên Cho Học Sinh
Cách Học Hiệu Quả
- Nắm vững khái niệm cơ bản
- Làm nhiều bài tập đa dạng
- Học từ đơn giản đến phức tạp
- Liên hệ với kiến thức đã học
Cách Ôn Thi
- Tổng hợp công thức quan trọng
- Phân loại dạng bài tập
- Luyện tập với đề thi thử
- Tìm hiểu các phương pháp giải nhanh
Kết Luận
Đường thẳng song song với mặt phẳng là một chủ đề quan trọng trong hình học không gian. Việc nắm vững kiến thức này không chỉ giúp học sinh đạt điểm cao trong các kỳ thi mà còn có nhiều ứng dụng thực tiễn trong cuộc sống.
Thông Tin Tuyển Sinh 24H
- Địa chỉ: 73 Nguyễn Chí Thanh, Láng Hạ, Đống Đa, Hà Nội
- Hotline: 0979 533 920 – 024.3200 5561
- Văn phòng tuyển sinh: 024.3200 5561
Để biết thêm thông tin chi tiết về các khóa học và tài liệu ôn tập, vui lòng truy cập website baogiaoduc24h.com hoặc liên hệ trực tiếp với chúng tôi qua các kênh thông tin trên.