Giới Thiệu
Phép Suy Đồ Thị: Khám Phá Chi Tiết và Ứng Dụng là một kỹ năng quan trọng trong toán học, đặc biệt hữu ích trong các bài toán phân tích và ứng dụng thực tế. Việc hiểu và áp dụng các phép suy đồ thị giúp học sinh, sinh viên nắm vững cách biến đổi và phân tích các hàm số, từ đó giải quyết các bài toán một cách hiệu quả. Trong bài viết này, Thông Tin Tuyển Sinh 24H sẽ giới thiệu chi tiết về phép suy đồ thị, các phương pháp và ví dụ minh họa cụ thể.
Phép suy đồ thị là quá trình biến đổi một đồ thị hàm số ban đầu thành một đồ thị mới thông qua các phép biến đổi như tịnh tiến, đối xứng, co giãn, và quay. Các phép biến đổi này giúp chúng ta hiểu rõ hơn về tính chất của hàm số và cách chúng thay đổi khi các biến số thay đổi.
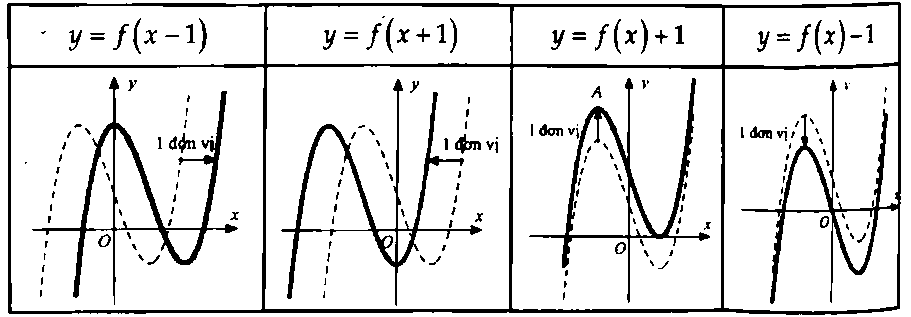
Các Phép Biến Đổi Đồ Thị Cơ Bản Tịnh Tiến Đồ Thị:
Tịnh tiến theo trục tung: Đồ thị của hàm số ( y = f(x) + a ) là kết quả của việc tịnh tiến đồ thị ( y = f(x) ) lên trên (nếu ( a ) dương) hoặc xuống dưới (nếu ( a ) âm) một khoảng ( a ) đơn vị.
Tịnh tiến theo trục hoành: Đồ thị của hàm số ( y = f(x + b) ) là kết quả của việc tịnh tiến đồ thị ( y = f(x) ) sang trái (nếu ( b ) dương) hoặc sang phải (nếu ( b ) âm) một khoảng ( b ) đơn vị.
Đối Xứng Đồ Thị:
Đối xứng qua trục tung: Đồ thị của hàm số ( y = f(-x) ) là kết quả của việc lấy đối xứng đồ thị ( y = f(x) ) qua trục tung.
Đối xứng qua trục hoành: Đồ thị của hàm số ( y = -f(x) ) là kết quả của việc lấy đối xứng đồ thị ( y = f(x) ) qua trục hoành.
Co Giãn Đồ Thị:
Co giãn theo trục tung: Đồ thị của hàm số ( y = kf(x) ) (với ( k > 1 )) là kết quả của việc co giãn đồ thị ( y = f(x) ) theo trục tung với hệ số ( k ).
Co giãn theo trục hoành: Đồ thị của hàm số ( y = f(kx) ) (với ( k > 1 )) là kết quả của việc co giãn đồ thị ( y = f(x) ) theo trục hoành với hệ số ( k ).
Quay Đồ Thị:
Đồ thị của hàm số ( y = f(ax + b) ) có thể được coi là kết quả của việc quay đồ thị ( y = f(x) ) quanh một điểm cố định.
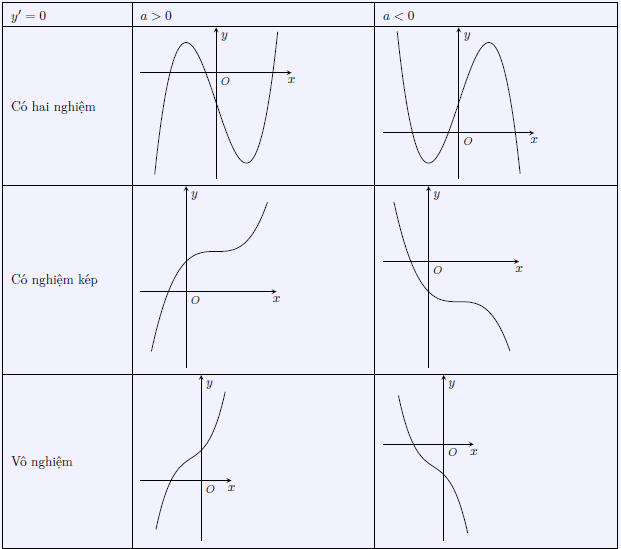
Ví Dụ Minh Họa
Ví Dụ 1: Tịnh Tiến Đồ Thị
Cho hàm số ( y = f(x) = x^2 ). Hãy vẽ đồ thị của hàm số ( y = f(x) + 3 ).
Giải: Đồ thị của hàm số ( y = x^2 ) là một parabol mở lên với đỉnh tại gốc tọa độ (0, 0). Khi tịnh tiến đồ thị này lên trên 3 đơn vị, ta được đồ thị của hàm số ( y = x^2 + 3 ), với đỉnh tại điểm (0, 3).
Ví Dụ 2: Đối Xứng Đồ Thị
Cho hàm số ( y = f(x) = \sqrt{x} ). Hãy vẽ đồ thị của hàm số ( y = f(-x) ).
Giải: Đồ thị của hàm số ( y = \sqrt{x} ) là một đường cong bắt đầu từ gốc tọa độ và mở rộng về phía bên phải. Khi lấy đối xứng đồ thị này qua trục tung, ta được đồ thị của hàm số ( y = \sqrt{-x} ), mở rộng về phía bên trái.
Ví Dụ 3: Co Giãn Đồ Thị
Cho hàm số ( y = f(x) = \sin(x) ). Hãy vẽ đồ thị của hàm số ( y = 2\sin(x) ).
Giải: Đồ thị của hàm số ( y = \sin(x) ) là một đường sóng hình sin với biên độ 1. Khi co giãn đồ thị này theo trục tung với hệ số 2, ta được đồ thị của hàm số ( y = 2\sin(x) ), với biên độ 2.
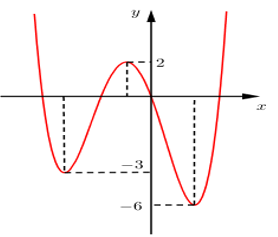
Ứng Dụng Của Phép Suy Đồ Thị
Phép suy đồ thị không chỉ là một công cụ hữu ích trong toán học mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác như vật lý, kinh tế, và kỹ thuật. Ví dụ, trong vật lý, các phép biến đổi đồ thị giúp chúng ta hiểu rõ hơn về các hiện tượng sóng, dao động và chuyển động. Trong kinh tế, chúng giúp phân tích các xu hướng và dự đoán sự biến động của thị trường.
Tài Liệu Tham Khảo
Để nắm vững hơn về phép suy đồ thị và các ứng dụng của nó, bạn có thể tham khảo các tài liệu và bài viết trên baogiaoduc24h.com. Đây là một nguồn tài liệu phong phú và đáng tin cậy, cung cấp nhiều thông tin hữu ích cho học sinh, sinh viên và giáo viên.
Kết Luận
Phép suy đồ thị là một kỹ năng quan trọng và hữu ích trong toán học và các lĩnh vực liên quan. Việc hiểu và áp dụng các phép biến đổi đồ thị giúp chúng ta giải quyết các bài toán một cách hiệu quả và chính xác hơn. Thông Tin Tuyển Sinh 24H hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức cần thiết về phép suy đồ thị và cách áp dụng chúng trong thực tế. Đừng quên tham khảo thêm các tài liệu trên baogiaoduc24h.com để nâng cao kiến thức và kỹ năng của mình.
Nếu bạn có bất kỳ câu hỏi nào hoặc cần thêm thông tin, hãy liên hệ với chúng tôi. Chúc bạn học tập tốt và thành công!
